Thanks to F-GAN, which established the general framework of GAN training, recently we saw modifications of GAN which unlike the original GAN, learn other metrics other than Jensen-Shannon divergence (JSD).
One of those modifications are Wasserstein GAN (WGAN), which replaces JSD with Wasserstein distance. It works wonderfully well and even the authors claimed that it cures the mode collapse problem and providing GAN with meaningful loss function. Although the implementation is quite straightforward, the theory behind WGAN is heavy and requires some “hack” e.g. weight clipping. Moreover, the training process and the convergence are slower than the original GAN.
Now, the question is: could we design GAN that works well, fast, simpler, and more intuitive compared to WGAN?
The answer yes. What we need is to back to basic.
Least Squares GAN
The main idea of LSGAN is to use loss function that provides smooth and non-saturating gradient in discriminator
As we know in original GAN,
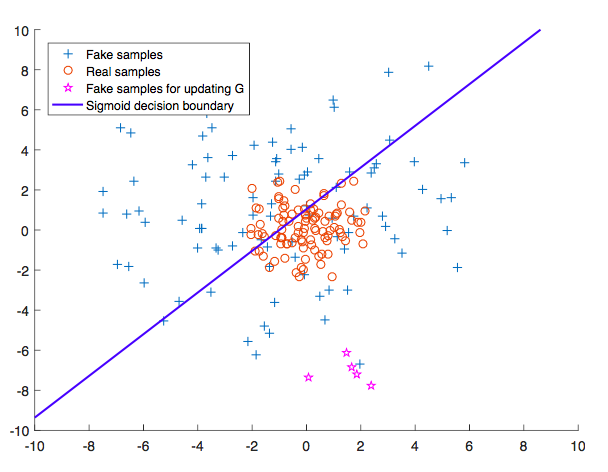
As
For learning the manifold of
Enter
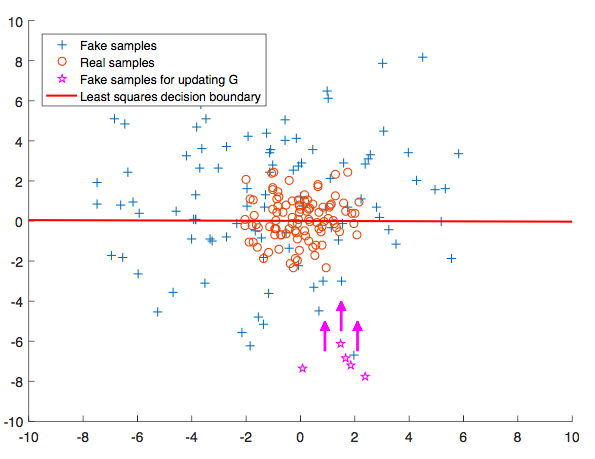
In
During the optimization process, the only way for
The overall training objective of LSGAN then could be stated as follows:
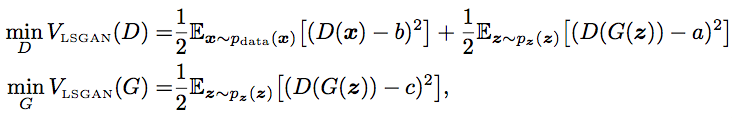
Above, we choose
Those values is not the only valid values, though. The authors of LSGAN provides some theory that optimizing the above loss is the same as minimizing Pearson
Our final loss is as follows:
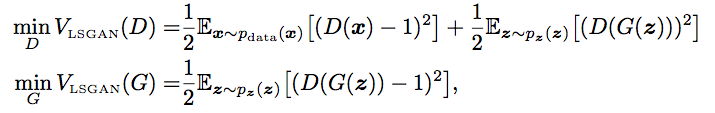
LSGAN implementation in Pytorch
Let’s outline the modifications done by LSGAN to the original GAN:
- Remove
- Use
So let’s begin by doing the the first checklist:
G = torch.nn.Sequential( torch.nn.Linear(z_dim, h_dim), torch.nn.ReLU(), torch.nn.Linear(h_dim, X_dim), torch.nn.Sigmoid())
D = torch.nn.Sequential( torch.nn.Linear(X_dim, h_dim), torch.nn.ReLU(), # No sigmoid torch.nn.Linear(h_dim, 1),)
G_solver = optim.Adam(G.parameters(), lr=lr)D_solver = optim.Adam(D.parameters(), lr=lr)The rest is straightforward, following the loss function above.
for it in range(1000000): # Sample data z = Variable(torch.randn(mb*size, z_dim)) X, * = mnist.train.next_batch(mb_size) X = Variable(torch.from_numpy(X))
# Dicriminator G_sample = G(z) D_real = D(X) D_fake = D(G_sample)
# Discriminator loss D_loss = 0.5 * (torch.mean((D_real - 1)**2) + torch.mean(D_fake**2))
D_loss.backward() D_solver.step() reset_grad()
# Generator G_sample = G(z) D_fake = D(G_sample)
# Generator loss G_loss = 0.5 * torch.mean((D_fake - 1)**2)
G_loss.backward() G_solver.step() reset_grad()The full code is available at https://github.com/wiseodd/generative-models.
Conclusion
In this post we looked at LSGAN, which modifies the original GAN by using
We looked at the intuition why
Finally, we implemented LSGAN in Pytorch. We found that the implementation of LSGAN is very simple, amounting to just two line changes.
References
- Nowozin, Sebastian, Botond Cseke, and Ryota Tomioka. “f-GAN: Training generative neural samplers using variational divergence minimization.” Advances in Neural Information Processing Systems. 2016. arxiv
- Mao, Xudong, et al. “Multi-class Generative Adversarial Networks with the L2 Loss Function.” arXiv preprint arXiv:1611.04076 (2016). arxiv