/ 8 min read

Modern Arts of Laplace Approximations

Let defined by be a neural network, where , , and be the input, parameter, and output spaces, respectively. Given a dataset , we define the likelihood . Then, given a prior , we can obtain the posterior via an application of Bayes’ rule: . But, the exact computation of is intractable in general due to the need of computing the normalization constant

We must then approximate . One simple way to do this is by simply finding one single likeliest point under the posterior, i.e. the mode of . This can be done via optimization, instead of integration:

The estimate is referred to as the maximum a posteriori (MAP) estimate. However, the MAP estimate does not capture the uncertainty around . Thus, it often (and in some cases, e.g. [1], almost always) leads to overconfidence.

In the context of Bayesian neural networks, the Laplace approximation (LA) is a family of methods for obtaining a Gaussian approximate posterior distribution of networks’ parameters. The fact that it produces a Gaussian approximation is a step up from the MAP estimation: particularly, it conveys some notion of uncertainty in . LA stems from the early work of Pierre-Simon Laplace in 1774 [2] and it was first adapted for Bayesian neural networks (BNNs) by David MacKay in 1992 [3]. The method goes as follows.

Given the MAP estimate , let us Taylor-expand around up to the second-order:

(Note that the gradient is zero at since is a critical point of and thus the first-order term in the above is also zero.) Now, recall that is the log-numerator of the posterior . Thus, the r.h.s. of the above can be used to approximate the true numerator, by simply exponentiating it:

For simplicity, let . Then, using this approximation, we can also obtain an approximation of :

where the equality follows from the fact the integral above is the famous, tractable Gaussian integral. Combining both approximations, we obtain

That is, we obtain a tractable, easy-to-work-with Gaussian approximation to the intractable posterior via a simple second-order Taylor expansion! Moreover, this is not just any Gaussian approximation: Notice that this Gaussian is fully determined once we have the MAP estimate . Considering that the MAP estimation is the standard procedure for training NNs, the LA is nothing but a simple post-training step on top of it. This means the LA, unlike other approximate inference methods, is a post-hoc method that can be applied to virtually any pre-trained NN, without the need of re-training!

Given this approximation, we can then use it as a proxy to the true posterior. For instance, we can use it to obtain the predictive distribution

which in general is less overconfident compared to the MAP-estimate-induced predictive distribution [3].

What we have seen is the most general framework of the LA. One can make a specific design decision, such as by imposing a special structure to the Hessian , and thus the covariance .

The laplace-torch library

The simplicity of the LA is not without a drawback. Recall that the parameter is in . In neural networks (NNs), is often in the order of millions or even billions. Naively computing the Hessian is thus often infeasible since it scales like . Together with the fact that the LA is an old method (and thus not “trendy” in the (Bayesian) deep learning community), this might be the reason why the LA is not as popular as other BNN posterior approximation methods such as variational Bayes (VB) and Markov Chain Monte Carlo (MCMC).

Motivated by this observation, in our NeurIPS 2021 paper titled “Laplace Redux – Effortless Bayesian Deep Learning”, we showcase that (i) the Hessian can be obtained cheaply, thanks to recent advances in second-order optimization, and (ii) even the simplest LA can be competitive to more sophisticated VB and MCMC methods, while only being much cheaper than them. Of course, numbers alone are not sufficient to promote the goodness of the LA. So, in that paper, we also propose an extendible, easy-to-use software library for PyTorch called laplace-torch, which is available at this Github repo.

The laplace-torch is a simple library for, essentially, “turning standard NNs into BNNs”. The main class of this library is the class Laplace, which can be used to transform a standard PyTorch model into a Laplace-approximated BNN. Here is an example.

try_laplace.py
from laplace import Laplace


model = load_pretrained_model()
la = Laplace(model, 'regression')


# Compute the Hessian
la.fit(train_loader)


# Hyperparameter tuning
la.optimize_prior_precision()


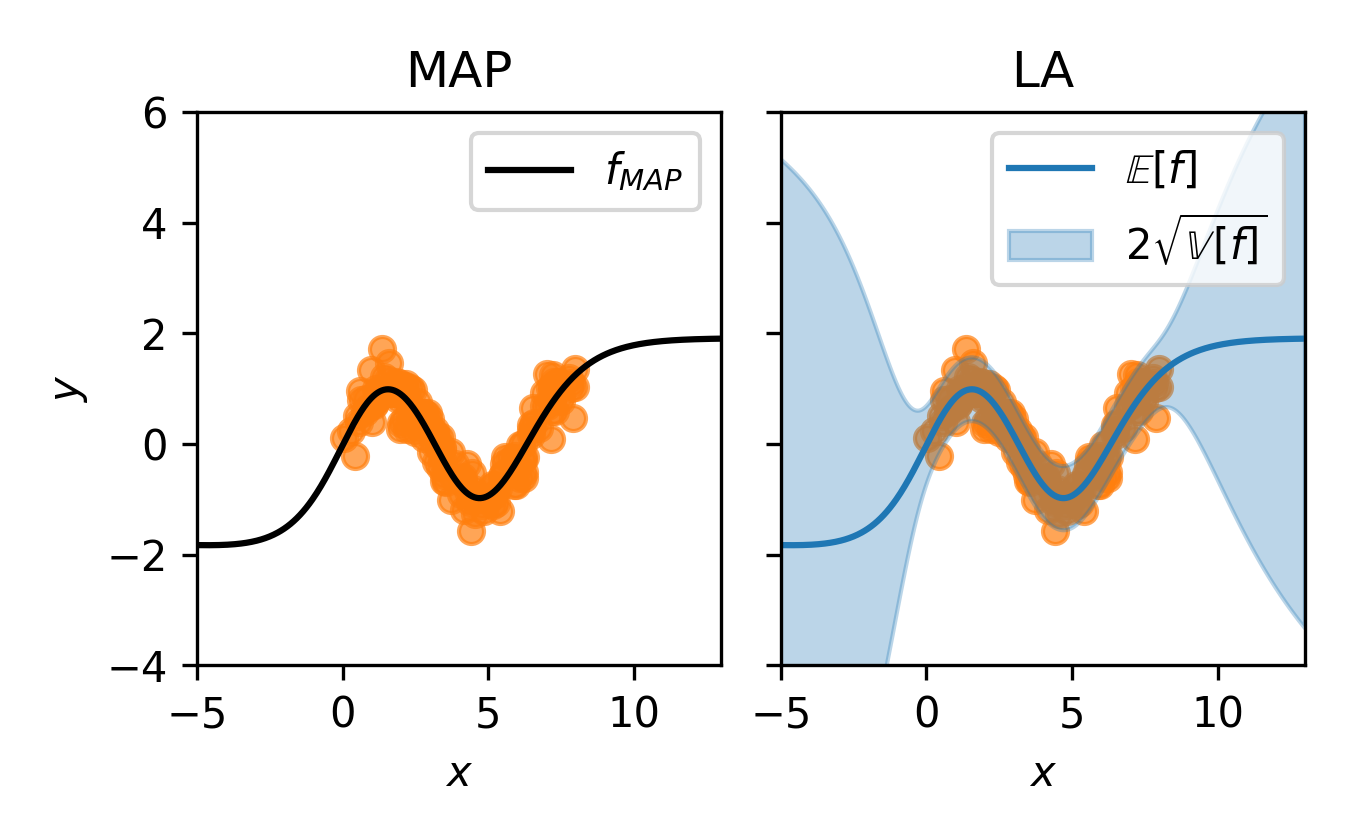
# Make prediction
pred_mean, pred_var = la(x_test)

The resulting object, la is a fully-functioning BNN, yielding the following prediction. (Notice the identical regression curves—the LA essentially imbues MAP predictions with uncertainty estimates.)

Laplace for regression.
Fig.   Laplace for regression.

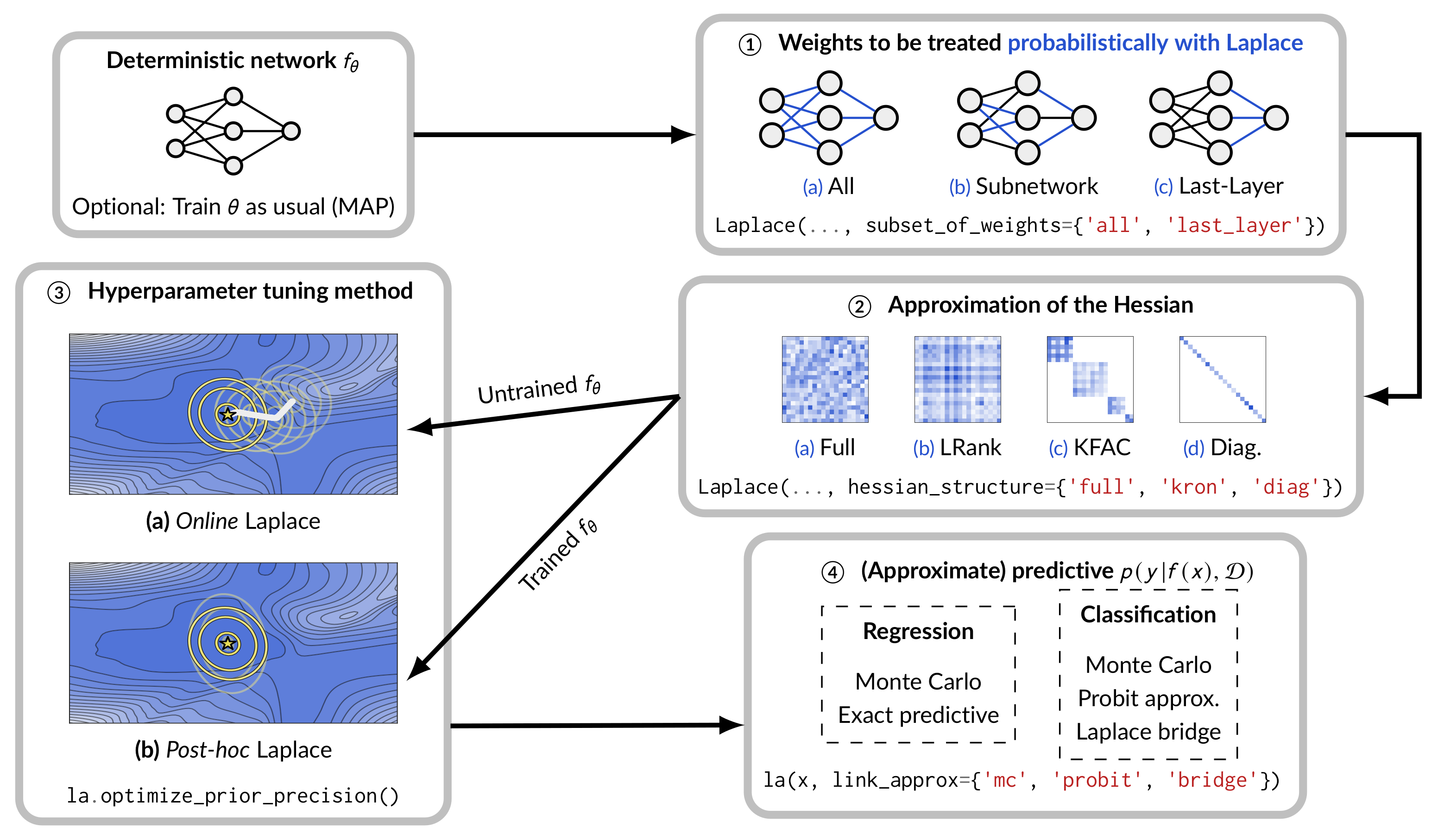
Of course, laplace-torch is flexible: the Laplace class has almost all state-of-the-art features in Laplace approximations. Those features, along with the corresponding options in laplace-torch, are summarized in the following flowchart. (The options 'subnetwork' for subset_of_weights and 'lowrank' for hessian_structure are in the work, by the time this post is first published.)

Modern arts of Laplace approximations.
Fig.   Modern arts of Laplace approximations.

The laplace-torch library uses a very cheap yet highly-performant flavor of LA by default, based on [4]:

def Laplace(model, likelihood, subset_of_weights='last_layer', hessian_structure='kron', ...)

That is, by default the Laplace class will fit a last-layer Laplace with a Kronecker-factored Hessian for approximating the covariance. Let us see how this default flavor of LA performs compared to the more sophisticated, recent (all-layer) Bayesian baselines in classification.

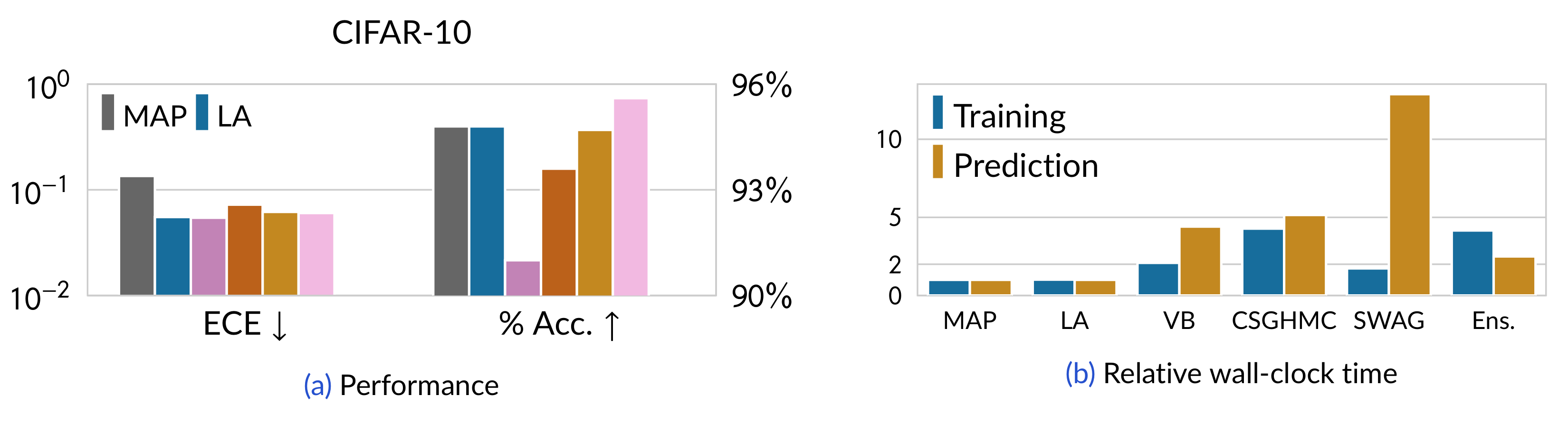
Laplace for classification.
Fig.   Laplace for classification.

Here we can see that Laplace, with default options, improves the calibration (in terms of expected calibration error (ECE)) of the MAP model. Moreover, it is guaranteed to preserve the accuracy of the MAP model—something that cannot be said for other baselines. Ultimately, this improvement is cheap: laplace-torch only incurs little overhead relative to the MAP model—far cheaper than other Bayesian baselines.

Hyperparameter Tuning

Hyperparameter tuning, especially for the prior variance/precision, is crucial in modern Laplace approximations for BNNs. laplace-torch provides several options: (i) cross-validation and (ii) marginal-likelihood maximization (MLM, also known as empirical Bayes and type-II maximum likelihood).

Cross-validation is simple but needs a validation dataset. In laplace-torch, this can be done via the following.

la.optimize_prior_precision(method='CV', val_loader=val_loader)

A more sophisticated and interesting tuning method is MLM. Recall that by taking the second-order Taylor expansion over the log-posterior, we obtain an approximate normalization constant of the Gaussian approximate posterior. This object is called the marginal likelihood: it is a probability over the dataset and crucially, it is a function of the hyperparameter since the parameter is marginalized out. Thus, we can find the best values for our hyperparameters by maximizing this function.

In laplace-torch, the marginal likelihood can be accessed via

ml = la.log_marginal_likelihood(prior_precision)

This function is compatible with PyTorch’s autograd, so we can backpropagate through it to obtain the gradient of w.r.t. the prior precision hyperparameter:

ml.backward()  # Works!

Thus, MLM can easily be done in laplace-torch. By extension, recent methods such as online MLM [5], can also easily be applied using laplace-torch.

Outlooks

The laplace-torch library is continuously developed. Support for more likelihood functions and priors, subnetwork Laplace, etc. are on the way.

In any case, we hope to see the revival of the LA in the Bayesian deep learning community. So, please try out our library at https://github.com/AlexImmer/Laplace!

References

  1. Hein, Matthias, Maksym Andriushchenko, and Julian Bitterwolf. “Why ReLU networks yield high-confidence predictions far away from the training data and how to mitigate the problem.” CVPR 2019.
  2. Laplace, Pierre Simon. “Mémoires de Mathématique et de Physique, Tome Sixieme” 1774.
  3. MacKay, David JC. “The evidence framework applied to classification networks.” Neural computation 4.5 (1992).
  4. Kristiadi, Agustinus, Matthias Hein, and Philipp Hennig. “Being Bayesian, even just a bit, fixes overconfidence in ReLU networks.” ICML 2020.
  5. Immer, Alexander, Matthias Bauer, Vincent Fortuin, Gunnar Rätsch, and Mohammad Emtiyaz Khan. “Scalable marginal likelihood estimation for model selection in deep learning.” ICML, 2021.