/ 6 min read

Conditional Variational Autoencoder: Intuition and Implementation

Conditional Variational Autoencoder (CVAE) is an extension of Variational Autoencoder (VAE), a generative model that we have studied in the last post. We’ve seen that by formulating the problem of data generation as a bayesian model, we could optimize its variational lower bound to learn the model.

However, we have no control on the data generation process on VAE. This could be problematic if we want to generate some specific data. As an example, suppose we want to convert a unicode character to handwriting. In vanilla VAE, there is no way to generate the handwriting based on the character that the user inputted. Concretely, suppose the user inputted character ‘2’, how do we generate handwriting image that is a character ‘2’? We couldn’t.

Hence, CVAE [1] was developed. Whereas VAE essentially models latent variables and data directly, CVAE models lantent variables and data, both conditioned to some random variables.

Conditional Variational Autoencoder

Recall, on VAE, the objective is:

that is, we want to optimize the log likelihood of our data under some “encoding” error. The original VAE model has two parts: the encoder and the decoder .

Looking closely at the model, we could see why can’t VAE generate specific data, as per our example above. It’s because the encoder models the latent variable directly based on , it doesn’t care about the different type of . For example, it doesn’t take any account on the label of .

Similarly, in the decoder part, it only models directly based on the latent variable .

We could improve VAE by conditioning the encoder and decoder to another thing(s). Let’s say that other thing is , so the encoder is now conditioned to two variables and : . The same with the decoder, it’s now conditioned to two variables and : .

Hence, our variational lower bound objective is now in this following form:

i.e. we just conditioned all of the distributions with a variable .

Now, the real latent variable is distributed under . That is, it’s now a conditional probability distribution (CPD). Think about it like this: for each possible value of , we would have a . We could also use this form of thinking for the decoder.

CVAE: Implementation

The conditional variable could be anything. We could assume it comes from a categorical distribution expressing the label of our data, gaussian expressing some regression target, or even the same distribution as the data (e.g. for image inpainting: conditioning the model to incomplete image).

Let’s use MNIST for example. We could use the label as our conditional variable . In this case, is categorically distributed, or in other words, it takes form as an one-hot vector of label:

mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
X_train, y_train = mnist.train.images, mnist.train.labels
X_test, y_test = mnist.test.images, mnist.test.labels


m = 50
n_x = X_train.shape[1]
n_y = y_train.shape[1]
n_z = 2
n_epoch = 20


# Q(z|X,y) -- encoder
X = Input(batch_shape=(m, n_x))
cond = Input(batch_shape=(m, n_y))

The natural question to arise is how do we incorporate the new conditional variable into our existing neural net? Well, let’s do the simplest thing: concatenation.

inputs = merge([X, cond], mode='concat', concat_axis=1)


h_q = Dense(512, activation='relu')(inputs)
mu = Dense(n_z, activation='linear')(h_q)
log_sigma = Dense(n_z, activation='linear')(h_q)

Similarly, the decoder is also concatenated with the conditional vector:

def sample_z(args):
    mu, log_sigma = args
    eps = K.random_normal(shape=(m, n_z), mean=0., std=1.)
    return mu + K.exp(log_sigma / 2) * eps


# Sample z ~ Q(z|X,y)
z = Lambda(sample_z)([mu, log_sigma])
z_cond = merge([z, cond], mode='concat', concat_axis=1) # <--- NEW!


# P(X|z,y) -- decoder
decoder_hidden = Dense(512, activation='relu')
decoder_out = Dense(784, activation='sigmoid')


h_p = decoder_hidden(z_cond)
outputs = decoder_out(h_p)

The rest is similar to VAE. Heck, even we don’t need to modify the objective. Everything is already expressed in our neural net models.

def vae_loss(y_true, y_pred):
    """ Calculate loss = reconstruction loss + KL loss for each data in minibatch """
    # E[log P(X|z,y)]
    recon = K.sum(K.binary_crossentropy(y_pred, y_true), axis=1)
    # D_KL(Q(z|X,y) || P(z|X)); calculate in closed form as both dist. are Gaussian
    kl = 0.5 * K.sum(K.exp(log_sigma) + K.square(mu) - 1. - log_sigma, axis=1)


    return recon + kl

For the full explanation of the code, please refer to my original VAE post. The full code could be found in my Github repo: https://github.com/wiseodd/generative-models.

Conditional MNIST

We will test our CVAE model to generate MNIST data, conditioned to its label. With the above model, we could specify which digit we want to generate, as it is conditioned to the label!

First thing first, let’s visualize :

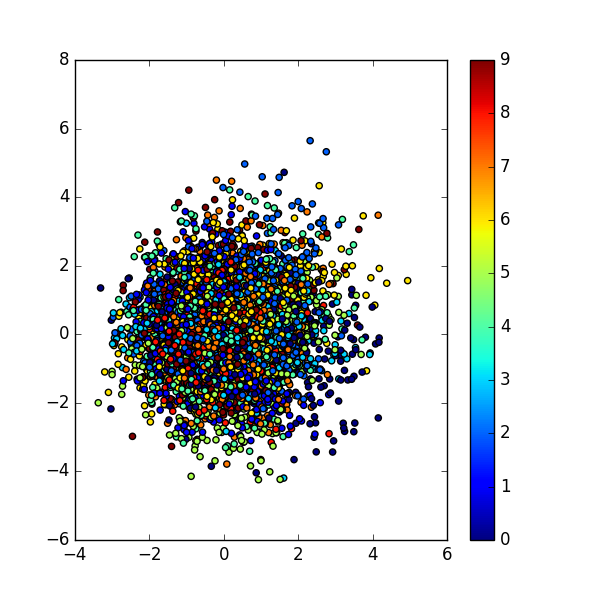
Things are messy here, in contrast to VAE’s , which nicely clusters . But if we look at it closely, we could see that given a specific value of , is roughly ! It’s because, if we look at our objective above, we are now modeling , which we infer variationally with a .

Next, let’s try to reconstruct some images:

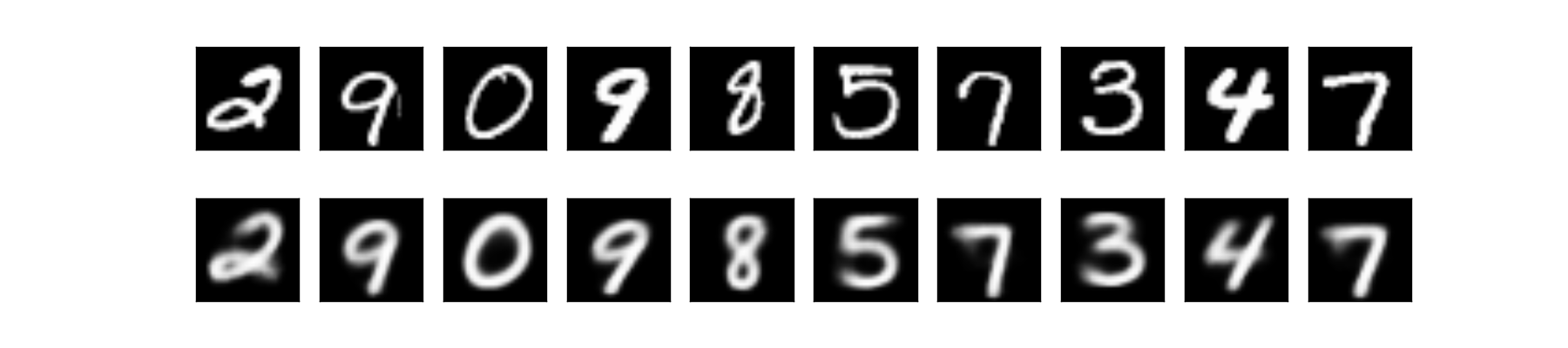
Subjectively, we could say the reconstruction results are way better than the original VAE! We could argue that because each data under specific label has its own distribution, hence it is easy to sample data with a specific label. If we look back at the result of the original VAE, the reconstructions suffer at the edge cases, e.g. when the model is not sure if it’s 3, 8, or 5, as they look very similar. No such problem here!

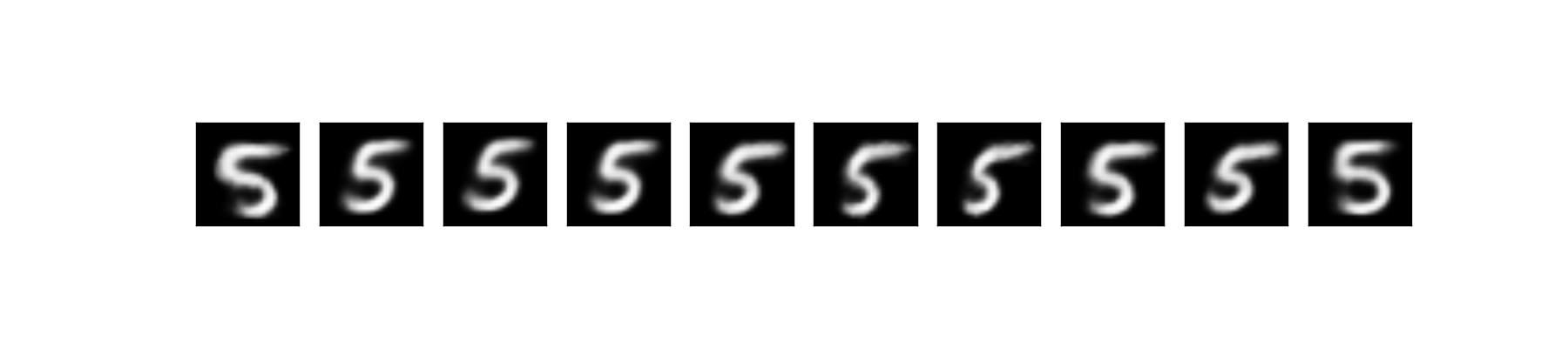
Now the interesting part. We could generate a new data under our specific condition. Above, for example, we generate new data which has the label of ‘5’, i.e. . CVAE make it possible for us to do that.

Conclusion

In this post, we looked at the extension of VAE, the Conditional VAE (CVAE).

In CVAE, we could generate data with specific attribute, an operation that can’t be done with the vanilla VAE. We showed this by applying CVAE on MNIST data and conditioned the model to the images’ labels. The resulting model allows us to sample data under specific label.

We also noticed that by conditioning our MNIST data to their labels, the reconstruction results is much better than the vanilla VAE’s. Hence, it is a good thing, to incorporate labels to VAE, if available.

Finally, CVAE could be conditioned to anything we want, which could result on many interesting applications, e.g. image inpainting.

References

  1. Sohn, Kihyuk, Honglak Lee, and Xinchen Yan. “Learning Structured Output Representation using Deep Conditional Generative Models.” Advances in Neural Information Processing Systems. 2015.